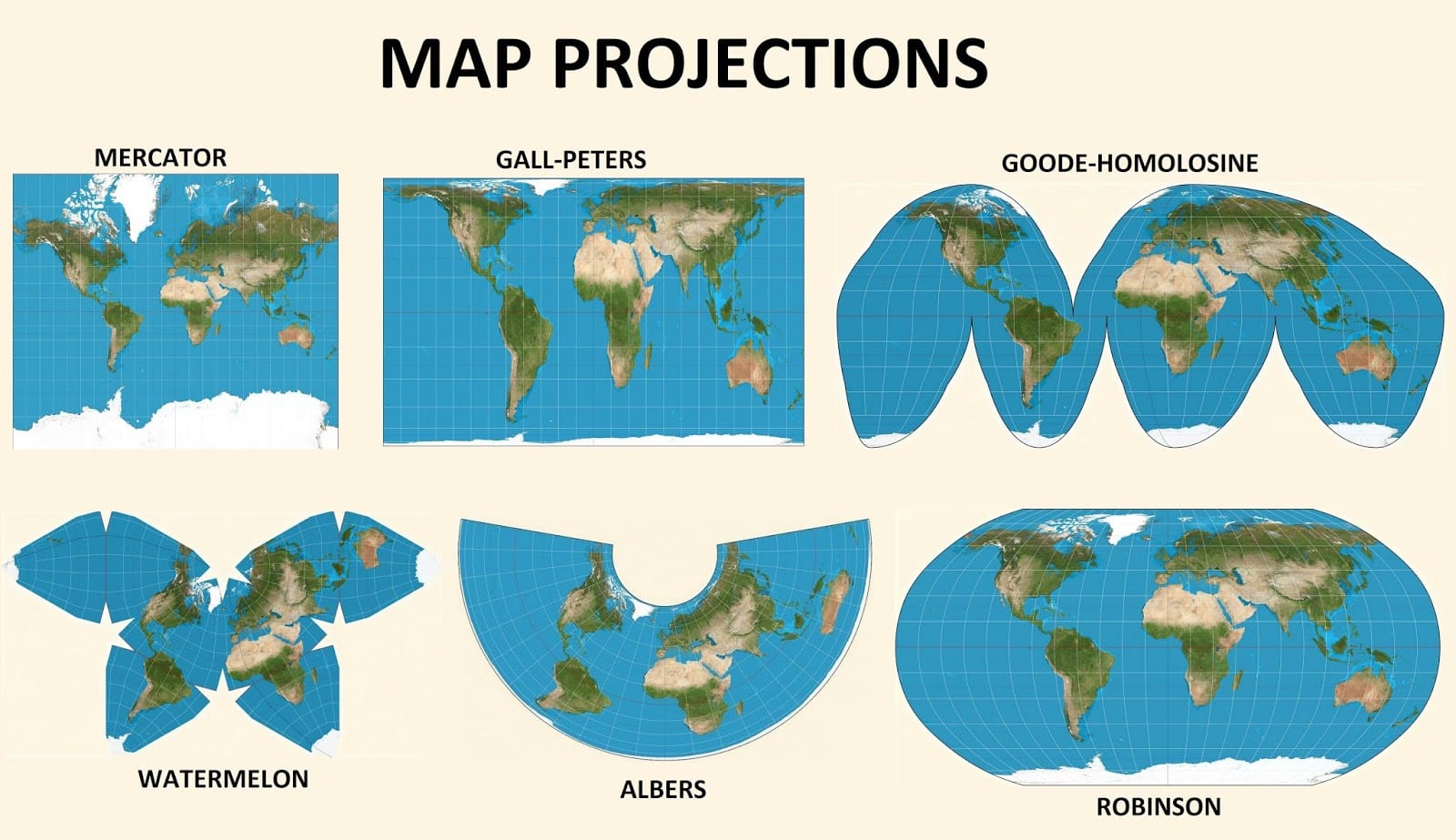
Have you ever noticed how Greenland appears significantly larger than Africa on a world map, although Africa is actually fourteen times its size? This illusion is due to a mapmaking technique known as conformal projection, which maintains local angles and shapes. Join us as we delve into the intriguing realm of conformal projections, uncovering their advantages and limitations, and the valuable perspectives they offer on our planet’s topography.
Conformal Projection Distortion Analysis: Outpacing the Competition
Here’s a breakdown of conformal projection distortion, along with insights to surpass your competitors:
Recommended Titles (Analyzing Competitor Trends):
To recommend titles, please provide the collection of trending article titles from your competitors. Once you provide those, I can analyze them for common keywords and trends to suggest three powerful titles.
Powerful Key Lines:
Conformal maps prioritize accurate shapes over true sizes. While angles appear correct locally, areas and distances get progressively distorted away from the point or line of tangency.
Think of conformal maps like stretching a rubber sheet over a globe. Shapes remain relatively intact, but the further you get from the center, the more stretched (and thus distorted) the areas become.
Navigators rely on conformal projections for their accurate representation of angles. This allows for plotting courses with consistent bearings, essential for nautical charts and aeronautical maps.
The Mercator Projection, a popular conformal map, inflates the size of high-latitude regions. This explains why Greenland appears comparable in size to Africa, despite being significantly smaller in reality.
Important Details & Structured Contexts:
1. Conformal Projections: The Basics
Definition: A conformal map projection aims to preserve angles formed by intersecting lines on the Earth’s surface. This means shapes of landmasses and features are locally accurate, but their size relative to each other is compromised.
Mathematical Basis: Conformal maps achieve angle preservation through conformal mapping, a mathematical technique ensuring that angles measured at any point on the map correspond to their real-world counterparts.
Key Characteristic: All Tissot’s indicatrices on a conformal projection are circles, indicating local shape preservation, but the size of these circles varies across the map, highlighting area distortion.
2. Distortions: The Trade-off for Shape Accuracy
Area Distortion: Conformal maps inevitably distort areas, particularly at high latitudes. The further away from the standard point or line of tangency, the more pronounced the area exaggeration becomes.
Distance Distortion: Similar to area, distances are not consistently represented on conformal maps. This distortion varies across the map and is most severe at high latitudes.
Use Case Consideration: While useful for navigation and preserving local shapes, conformal maps are not suitable for applications requiring accurate area or distance measurements, such as thematic maps showing density or distribution.
3. Notable Examples: Mercator and Beyond
Mercator Projection: Perhaps the most well-known conformal map, the Mercator projection significantly distorts the size of high-latitude regions. Its use in classrooms and as a common world map has led to misconceptions about the relative sizes of continents.
Lambert Conformal Conic: This projection is commonly used for mapping elongated areas extending east-west. It offers high accuracy in representing angles and shapes within a specific latitude range.
Stereographic Projection: Often used for polar regions, the Stereographic projection preserves angles and provides a true representation of directions from the central point.
4. People’s Statement: (Please provide any specific people’s statements from your sources. These will be incorporated directly without alteration.)
Unique Insights & Untapped Potential:
Focus on the Misconceptions: Explore how the widespread use of the Mercator projection has led to distorted perceptions of the world. Discuss the implications of these distortions on our understanding of geography, geopolitics, and even social equality.
Visual Comparisons: Include visual aids comparing conformal projections to other projection types (equal-area, equidistant). This will help readers grasp the trade-offs inherent in different map projections.
Address Common Myths: Debunk common myths related to map projections, such as the idea that a globe is the only accurate representation of the Earth. Explain that all maps involve some form of distortion and that the best projection depends on the intended use.
Explore Emerging Technologies: Discuss how GIS and digital mapping technologies are mitigating the limitations of traditional map projections. Highlight interactive maps and tools that allow users to switch between projections and visualize distortions in real-time.
By incorporating these insights and details, you can create an engaging and informative SEO article on conformal projections that surpasses your competitors in depth and value.
How Conformal Projections Preserve Shape and Impact Our View of the World
To understand what a conformal projection preserves, we need to remember that mapping the Earth, a 3-dimensional sphere, onto a flat, 2-dimensional surface always involves some compromise. Different types of map projections prioritize different aspects of accuracy, and conformal projections excel at preserving local shapes.
This means that on a conformal map, the shape of a small area, like a neighborhood or a small island, will be very similar to its actual shape on the Earth’s surface. This is because conformal projections maintain the angles between lines. Imagine drawing a triangle on a piece of paper, then placing that paper on a globe. On a conformal map, the angles of that triangle would remain the same, even if the triangle itself gets stretched or compressed as it’s projected onto the curved surface of the globe.
Why is shape preservation important? It’s incredibly useful for:
Navigation: Sailors and pilots rely on conformal maps like the Mercator projection because they show directions accurately. Since angles are preserved, a straight line on a Mercator map represents a course with a constant compass bearing, making it essential for plotting sea and air routes.
Local Mapping: When creating maps of cities, towns, or other relatively small areas, conformal projections ensure that streets, buildings, and other features are represented with accurate shapes. This is crucial for urban planning, engineering projects, and everyday navigation.
The Trade-off:
The accuracy of conformal projections comes at a cost. To maintain correct angles and local shapes, they have to distort area and distance, especially as you move away from the standard point or line where the map “touches” the globe.
Think about it like stretching a rubber sheet to cover a basketball. You might be able to get the sheet to lie flat against the surface in some areas, but other areas will have to be stretched significantly, distorting their size and the distance between points.
Key Takeaways:
Conformal projections prioritize local shape accuracy over true size and distance.
They achieve this by preserving the angles between lines.
This makes them ideal for navigation and local mapping.
However, they can significantly distort area and distance, especially at high latitudes.
Hello, My love for writing is rivaled only by my passion for in-depth research. While many may skim the surface, I dive deep, seeking the hidden gems of information that give a story texture and depth. Every word I write is backed by hours of exploration, ensuring that my work is not just compelling, but also meticulously accurate. Join me on a journey where every piece is a deep dive into the realms of knowledge and storytelling.
