Ready to conquer the complexities of linear programming? This guide presents the interactive simplex tableau calculator, your indispensable tool for optimizing solutions. Forget manual calculations; embrace the power of automation and visualization to solve even the most intricate linear programming problems with ease. Whether you’re a seasoned mathematician or just starting out, this guide will equip you with the knowledge and resources to master the simplex method.
Understanding the Simplex Method and its Tableau
A simplex tableau calculator is a specialized tool designed to solve linear programming (LP) problems, which involve optimizing a linear objective function subject to linear constraints. Think of it as a supercharged spreadsheet tailored for the simplex method, a powerful algorithm used to find the best possible solution within given limitations. These limitations can be anything from available resources to budget constraints. The simplex method systematically explores the feasible region of the problem, moving from one feasible solution to another until it finds the optimal one. Want to learn more about Televisit? Click here for more information.
Constructing the Simplex Tableau
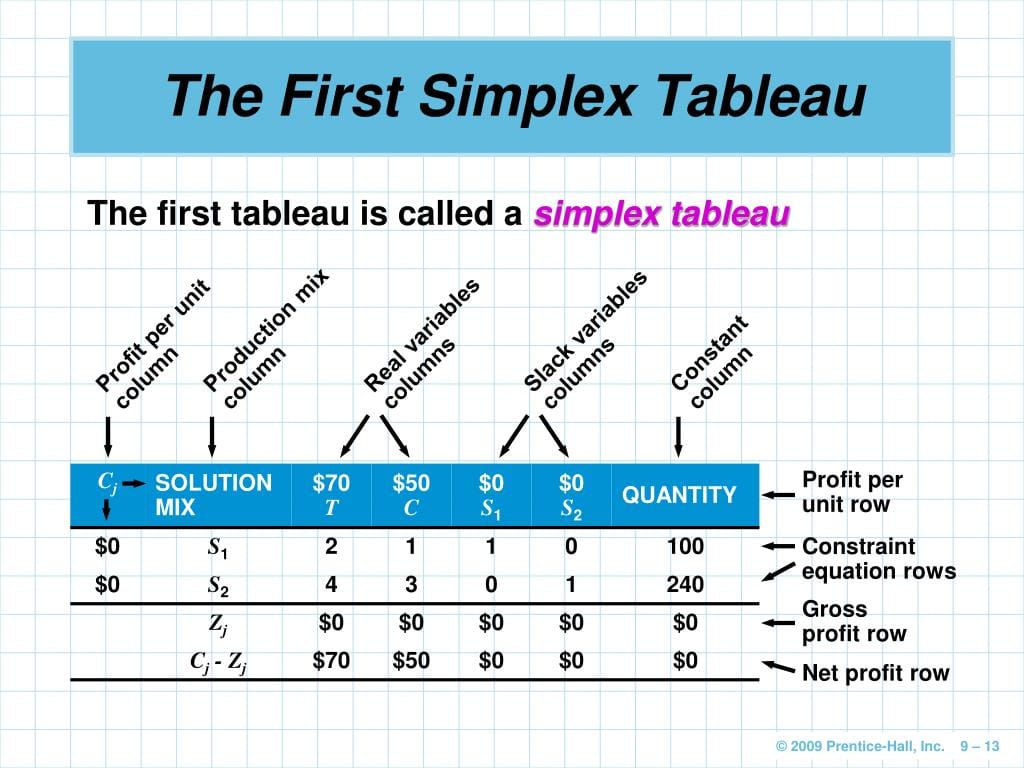
The first step is setting up the initial simplex tableau, a structured table that represents your LP problem. This involves:
- Defining the Problem: Clearly state your objective function (what you aim to maximize or minimize, such as profit or cost) and your constraints (limitations on resources, etc.).
- Converting Inequalities to Equalities: Introduce slack or surplus variables to transform inequality constraints (like “less than or equal to”) into equalities. These variables represent the unused portion of a resource or the amount by which a constraint is exceeded. They essentially help balance the equations.
- Adding Artificial Variables (If Necessary): For certain types of constraints (like “greater than or equal to”), artificial variables are introduced to create an initial feasible solution. These variables are typically used in the two-phase or Big M methods.
- Organizing the Tableau: Arrange the coefficients of the objective function and constraints in a tabular format, creating the initial simplex tableau.
The Pivoting Process: The Heart of the Simplex Method
The core of the simplex method is the pivoting process, a series of iterative steps that move towards the optimal solution:
- Identifying the Pivot Element: The pivot element is chosen strategically based on specific rules. For maximization problems, it’s often the most negative entry in the objective row. For minimization, it’s likely the most positive entry. The choice of pivot element influences the direction in which the algorithm searches for the optimal solution.
- Performing Row Operations: Elementary row operations are carried out using the pivot element. These operations transform the tableau, bringing the entering variable (represented by the pivot column) into the basis and removing a leaving variable. This process can be visualized as moving from one corner of the feasible region to another.
- Repeating Steps 1 and 2: The process of selecting a pivot element and performing row operations is repeated until an optimal solution is found. This iterative process gradually improves the objective function value while staying within the feasible region.
Handling Complexities: Two-Phase and Big M Methods
Some LP problems require special techniques:
- Two-Phase Method: This method is employed when artificial variables are present. Phase I minimizes the sum of artificial variables to find a feasible solution. Phase II then proceeds with the regular simplex method to optimize the original objective function, starting from the feasible solution found in Phase I.
- Big M Method: An alternative to the two-phase method, the Big M method assigns a large penalty (represented by “M”) to artificial variables in the objective function. This discourages the usage of artificial variables in the optimal solution. The algorithm then proceeds as usual, attempting to minimize this penalty while optimizing the original objective function. The “M” value is chosen to be significantly large enough to ensure that artificial variables are not part of the final optimal solution unless absolutely necessary.
Interpreting the Results
The final simplex tableau reveals the optimal solution:
- Optimal Solution: The values of the decision variables that optimize the objective function are found in the tableau.
- Optimal Objective Function Value: The maximum or minimum value of the objective function is also readily available in the final tableau.
- Infeasible or Unbounded Solutions: The tableau also helps identify cases where a feasible solution doesn’t exist (infeasible) or where the objective function can be improved indefinitely (unbounded). An infeasible solution suggests that the constraints are too restrictive, while an unbounded solution often indicates an error in the problem formulation.
Leveraging Interactive Simplex Tableau Calculators
Now that you understand the basics, let’s explore the power of interactive simplex tableau calculators. These online simplex calculators offer:
- Visualization: See the tableau transform in real-time with each pivot, gaining a deeper understanding of the process.
- Automation: Eliminate tedious manual calculations, reducing errors and saving time.
- Experimentation: Test different scenarios and explore the impact of changes on the solution.
- Flexibility: Handle a wide range of LP problems, from simple to complex, even those with hundreds or thousands of variables and constraints.
Step-by-Step Guide to Using an Interactive Simplex Tableau Calculator:
- Input Problem Data: Enter your objective function, constraints, and variables into the calculator. This might involve specifying whether you’re maximizing or minimizing the objective function.
- Visualize the Initial Tableau: The calculator generates the initial simplex tableau, clearly displaying the coefficients of your problem. This visual representation makes it easier to track the progress of the simplex method.
- Select Pivot Element (If Necessary): Some calculators automate this step. If required, select the pivot element based on the rules of the simplex method (most negative entry in the objective row for maximization problems, for instance).
- Perform Row Operations (Likely Automated): The calculator automatically performs the row operations, transforming the tableau toward the optimal solution. You might see these operations displayed step by step, further enhancing your understanding.
- Check for Optimality: The calculator identifies when an optimal solution is reached and displays the results. Some calculators might highlight the optimal values of the decision variables directly in the tableau, simplifying interpretation.
Benefits of Using Interactive Calculators
- Comprehensive understanding: Visualizing the steps reinforces your understanding of the simplex method.
- Effortless calculations: Automated row operations eliminate tedious computations and reduce errors.
- Enhanced problem-solving: Interactive exploration and experimentation deepen your analytical skills.
- Wide Applicability: Handle various LP problems, from simple to complex, across a range of fields.
Exploring Online Simplex Tableau Calculators and Resources
Several online tools are available:
- pmcalculators.com: Offers a two-phase simplex method calculator with detailed explanations.
- math.cmu.edu: Provides a tool for performing pivot operations on a tableau.
- lalith.dev: Features an interactive simplex algorithm solver.
- emathhelp.net: Handles slack, surplus, and artificial variables for diverse LP problems.
- zweigmedia.com: Provides a tool for solving linear programming problems.
- donisius.github.io: Supports both maximization and minimization problems.
- simplexsolver.xyz: A simplex optimization tool.
Interested in learning about the spots on dice and dominoes? Explore this fascinating topic here.
Beyond the Basics: Future Directions and Considerations
While the simplex method is a powerful tool, ongoing research explores more efficient algorithms, especially for extremely large-scale problems. Investigating these alternatives, like interior-point methods, can provide a broader perspective on the field of optimization. Additionally, understanding the connection between the simplex method and underlying linear algebra concepts can deepen your appreciation of its mathematical foundations.
By combining the power of the simplex method with the convenience and clarity of interactive calculators, you can confidently tackle optimization challenges in various fields, from business and finance to engineering and logistics. This guide provides a solid foundation for anyone seeking to master linear programming and unlock its potential.
- Unlock Water’s Symbolism: A Cross-Cultural Exploration - April 20, 2025
- Identify Black and White Snakes: Venomous or Harmless? - April 20, 2025
- Unlocking Potential: Origins High School’s NYC Story - April 20, 2025