Step into the world of linear programming and optimization with this comprehensive guide. Whether you’re a seasoned mathematician or just beginning your optimization journey, this guide will equip you with the knowledge and tools to conquer complex problems using the simplex method. Learn the core concepts and discover how simplex tableau calculators can become your trusty sidekick in finding optimal solutions.
Simplex Tableau Calculators: Your Optimization Assistant
Linear programming problems can be challenging. Finding the best solution often involves numerous calculations. Simplex tableau calculators simplify this process, acting as your personal assistant to reveal the optimal solution step-by-step. This guide provides a thorough understanding of these tools, covering both basic and advanced techniques.
Exploring Different Calculator Types
Simplex tableau calculators come in various forms, each designed for specific scenarios:
Two-Phase Method Calculators: These calculators are invaluable when dealing with initially infeasible problems, those that don’t seem to have a starting solution. They manage artificial variables, guiding you towards a feasible solution before optimization begins.
Generic Simplex Calculators: These are the versatile workhorses, ready to tackle a wide array of linear programming problems. Whether maximizing profits or minimizing costs, these calculators can handle diverse constraints and objective functions.
Interactive Tableau Tools: For those who want a deeper understanding of the simplex method’s inner workings, interactive tools offer a hands-on approach. You can manipulate the tableau directly, observing how each step in the process unfolds.
Understanding Calculator Functionality
Simplex tableau calculators offer a suite of features to streamline your workflow:
Input: Here, you enter the details of your problem, including the objective function (what you’re maximizing or minimizing), the constraints (your limitations), and the initial values.
Tableau Generation: The calculator constructs the initial simplex tableau based on your input. This structured table represents the problem mathematically, incorporating slack, surplus, or artificial variables as needed.
Pivoting and Iteration: The calculator performs iterative pivoting operations, systematically refining the tableau to approach the optimal solution. Many calculators display the intermediate tableaus, allowing you to trace the process.
Output: Finally, the calculator presents the optimal solution—the values for your decision variables that yield the best possible outcome. It also provides the corresponding optimal value of the objective function.
Using a Simplex Tableau Calculator: A Step-by-Step Approach
Grasp the Simplex Method Basics: While deep expertise isn’t required, a fundamental understanding of the simplex method is helpful for interpreting results and troubleshooting. Check out our How do you calculate the simplex method? guide for a primer.
Define Your Problem Precisely: Clearly articulate your objective function and constraints. Accurate problem formulation is essential for meaningful solutions. For help with structuring your problem, see our sample dbq.
Interpret the Results: Analyze the optimal solution and the tableau’s contents. This information empowers you to make informed decisions based on the calculator’s output. You may find our stem and leaf display calculator useful for visualizing your data.
Advanced Simplex Techniques
Big M Method: This technique addresses infeasible initial solutions by adding a penalty (represented by ‘M’) to the objective function for artificial variables. This penalty encourages the solution towards feasibility.
Two-Phase Method: When an initial feasible solution isn’t obvious, the two-phase method finds a feasible starting point before optimizing the objective function. It’s like clearing the path before starting your journey.
Tips for Simplex Success
Experiment with Calculators: Different calculators have different strengths. Find the one that best suits your needs and preferences.
Real-World Applications: Explore the simplex method’s practical applications across fields like business, economics, engineering, and science.
Create a Personalized Guide: Document your favorite calculator’s usage with a step-by-step guide and examples.
Integrate with Other Tools: Combine your simplex tableau calculator with other software for enhanced analysis.
Troubleshooting: Familiarize yourself with common errors and their solutions for a smooth workflow.
Harnessing Calculator Power for the Simplex Method
We’ve discussed the simplex method’s utility. Now, let’s explore its practical implementation using a calculator, especially beneficial for larger problems. Manual calculations can be tedious, but calculators streamline the process.
Using a graphing calculator for the simplex method is like having a superpower. It transforms a potentially complex process into a manageable task.
Your Step-by-Step Calculator Guide
Building the Tableau: The tableau is the arena for the simplex method, holding all the vital information. Carefully enter the coefficients from your objective function and constraints into the calculator’s matrix function. Double-check for accuracy, as typos can lead to errors.
Iterating Towards the Optimal Solution: The simplex method iteratively refines the solution. You select a “pivot” element and apply row operations (multiplying or dividing a row by a number) to transform the tableau. This process repeats until no negative numbers remain in the bottom row (the objective function row), signaling the optimal solution.
Navigating Infeasibility with the Two-Phase Method: Some problems are initially infeasible. The two-phase method introduces “artificial variables” as temporary placeholders, adjusting the objective function. After finding a feasible solution, the artificial variables are removed, and the standard simplex method continues.
Decimal Mode for Precision: Decimal mode minimizes rounding errors, ensuring accurate results. This setting maintains precision, providing reliable solutions.
Troubleshooting: Even with a calculator, errors can occur. Double-check your input and consult your calculator’s manual if issues arise.
Key Takeaways
Graphing calculators are powerful tools for solving linear programming problems with the simplex method.
Built-in functions and matrix operations reduce manual calculations.
The simplex method with calculator assistance handles complex problems efficiently.
Decimal mode ensures accuracy.
The two-phase method addresses initially infeasible problems.
While calculators simplify the process, understanding the underlying principles remains important. Ongoing research continuously refines optimization algorithms. Don’t hesitate to delve deeper into this dynamic field of mathematics. Continue your exploration with our guide on How to find pivot in simplex tableau calculator?.
Calculating the Simplex Method: A Step-by-Step Breakdown
Having established the foundation, let’s delve into the mechanics of the simplex method. The goal is to find the best solution (maximum or minimum) within given constraints.
The Simplex Method: A Building Process
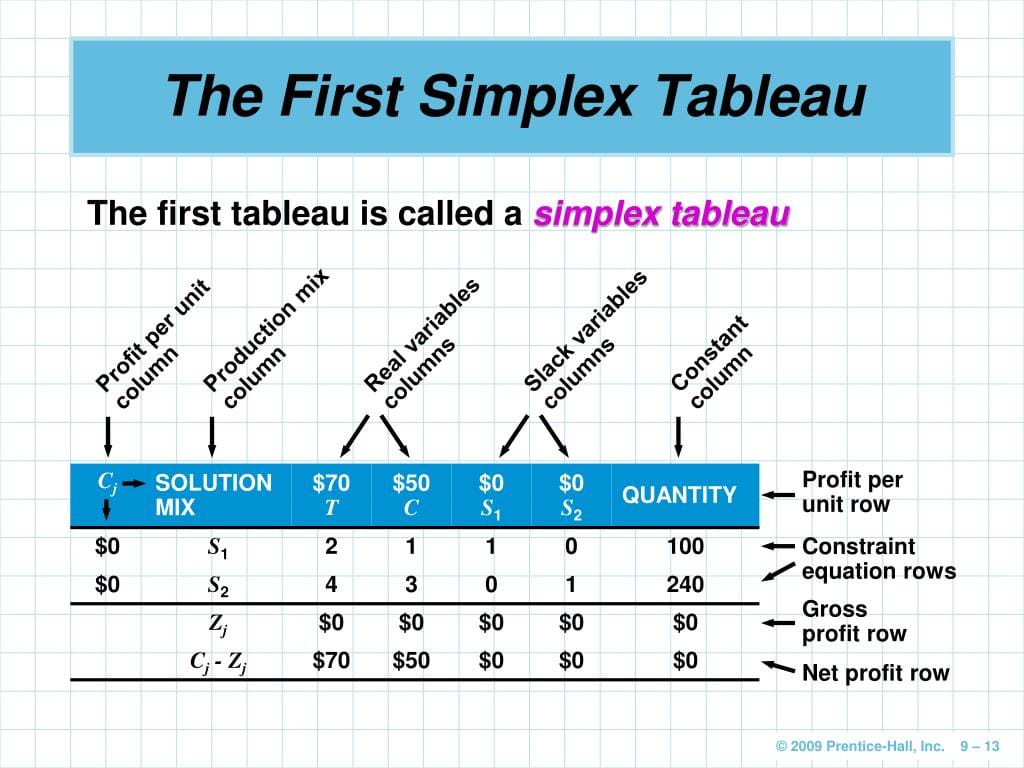
The simplex method utilizes a “tableau,” a structured table containing the problem’s information: the objective function (what we aim to maximize or minimize) and the constraints (our limitations). “Pivoting” is a key process involving selecting a “pivot element” and using it to manipulate other numbers in the tableau, bringing us closer to the optimal solution. This pivoting process repeats until we reach the optimal solution, indicated by the absence of negative numbers in a specific row of the tableau.
Step-by-Step Guide to the Simplex Method
Define the Problem: Clearly state the objective function and the constraints.
Build the Initial Tableau: Create the initial tableau to organize the problem’s information, utilizing “slack variables” to convert inequalities into equations.
Pivot and Iterate: Perform pivoting operations, selecting pivot elements and adjusting the tableau until the optimal solution is reached.
Find the Solution: Identify the optimal solution when a specific row (usually the bottom row representing the objective function) lacks negative numbers (except possibly the last column). The optimal variable values and the optimal objective function value are found within the final tableau.
Understanding the Simplex Method’s Nuances
Systematic Approach: The simplex method provides a structured, step-by-step approach.
Visual Representation: The tableau visually represents the problem and tracks changes.
Iterative Refinement: The process continuously refines the solution through iterations.
Clear Indication of Optimality: The absence of negative numbers in a specific row signals the optimal solution.
While powerful, the simplex method has limitations and advanced variations. Some problems have multiple or no solutions. “Degeneracy” can complicate the process. Ongoing research continues to refine simplex algorithms.
Finding the Pivot in a Simplex Tableau Calculator
You’re working with a simplex tableau and need to find the pivot element, a crucial step in the simplex method. This guide outlines the process.
Step-by-Step Pivot Identification
Spotting the Pivot Column: Examine the bottom row (objective row) and find the most negative number (ignoring the last entry – usually “RHS” or “Solution”). This column is your pivot column.
Calculating Ratios: For each row (except the bottom objective row), divide the entry in the far right column (solution column) by the corresponding entry in the pivot column. Skip rows with negative or zero values in the pivot column.
Pinpointing the Pivot Row: The row with the smallest positive ratio is the pivot row. The intersection of the pivot row and pivot column is the pivot element.
Pivoting – Tableau Transformation: Row operations are used to convert the pivot element to 1 and all other elements in the pivot column to 0.
Example
Consider this tableau:
x₁
x₂
x₃
x₄
RHS
z
-2
-3
0
0
0
s₁
1
2
1
0
6
s₂
0
1
0
1
3
Pivot Column: The most negative entry in the bottom row (excluding RHS) is -3, in the x₂ column.
Ratios:
Row s₁: 6 / 2 = 3
Row s₂: 3 / 1 = 3
Pivot Row: Since both ratios are equal, we can choose either. Selecting s₁ as the pivot row makes ‘2’ the pivot element.
Pivoting: Row operations would then be performed.
Additional Considerations
The simplex method is iterative; these steps are repeated until an optimal solution is found (no negative numbers in the bottom row except possibly the last entry). There can be complexities like unbounded or multiple optimal solutions. Research in optimization techniques is ongoing. Each pivot refines the solution towards the optimal outcome.
Hello, My love for writing is rivaled only by my passion for in-depth research. While many may skim the surface, I dive deep, seeking the hidden gems of information that give a story texture and depth. Every word I write is backed by hours of exploration, ensuring that my work is not just compelling, but also meticulously accurate. Join me on a journey where every piece is a deep dive into the realms of knowledge and storytelling.
1 thought on “Master the Simplex Method: A Guide to Simplex Tableau Calculators and Tools”
Comments are closed.