Navigating the world of parallel lines and transversals can feel like charting unknown territory, but with the right guide, it’s a journey of exciting discovery. This comprehensive guide will equip you with everything you need to confidently tackle these geometric concepts, from basic definitions to advanced problem-solving. We’ll explore the different types of angles formed, their relationships, and how to use this knowledge to solve for unknown values. Plus, we’ll provide links to a treasure trove of free printable worksheets and other helpful resources to solidify your understanding. Let’s get started!
Before diving into the specifics, let’s establish a solid foundation:
Parallel Lines: Imagine two perfectly straight train tracks extending infinitely – they never meet! That’s the essence of parallel lines: lines in a plane that never intersect, maintaining a constant distance between them.
Transversals: Now, picture a road intersecting those train tracks. That road acts as a transversal—a line that intersects two or more lines at distinct points.
When a transversal crosses parallel lines, it creates a fascinating interplay of angles, forming eight distinct angles with special relationships. Let’s explore these angles and their properties in more detail.
Decoding Angle Relationships
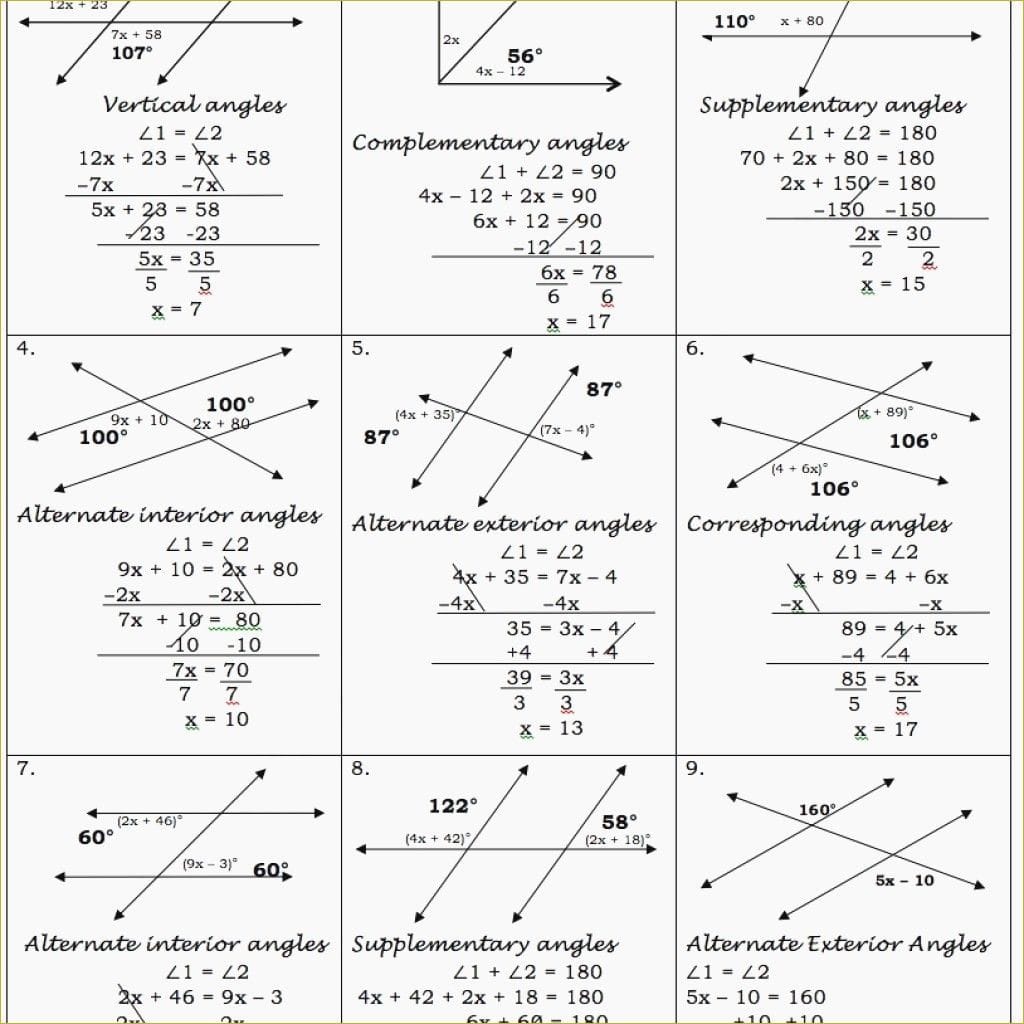
The intersection of a transversal and parallel lines produces eight angles, categorized into pairs with specific properties. Mastering these relationships is crucial for solving geometric problems.
1. Corresponding Angles
Imagine standing at one corner formed by the transversal and a parallel line, then teleporting to the identical corner on the other parallel line. The angles at these matching corners are corresponding angles. They’re like mirror images and are always congruent (equal in measure).
2. Alternate Interior Angles
These angles are nestled between the parallel lines and on opposite sides of the transversal. Think of them playing hide-and-seek! Like corresponding angles, alternate interior angles are also congruent.
3. Alternate Exterior Angles
Similar to alternate interior angles, these are on opposite sides of the transversal but reside outside the parallel lines. They, too, are always congruent.
These angles are located between the parallel lines and on the same side of the transversal. They are supplementary, meaning their measures add up to 180 degrees.
5. Vertical Angles
While not specific to parallel lines and transversals, vertical angles occur whenever two lines intersect. They are opposite each other and, like corresponding and alternate angles, are always congruent.
Putting Knowledge into Practice: Solving for Unknown Angles
Knowing the properties of these angle pairs is like having a secret decoder ring for geometry puzzles. If you know the measure of just one angle, you can often determine the measures of all the other angles formed by the transversal and parallel lines!
For example, if one corresponding angle measures 75 degrees, all other corresponding angles also measure 75 degrees. You can then use this information, along with the relationships between the other angle pairs (alternate interior, alternate exterior, consecutive interior, and vertical), to find the remaining angles.
Free Worksheets and Resources: Your Practice Toolkit
Practice is key to mastering any math concept, and parallel lines and transversals are no exception. That’s why we’ve compiled a selection of excellent free resources to help you hone your skills:
Printable Worksheets: Many websites offer free printable worksheets with varying difficulty levels and answer keys. Some recommended resources include:
Math Monks: Provides in-depth worksheets for grades 6-9 emphasizing angle relationship analysis and problem-solving. [Link to Math Monks Worksheets – Please Provide]
Math Worksheets 4 Kids: Printable worksheets with varying difficulty levels, including interior, exterior, and other angle types. [Link to Math Worksheets 4 Kids – Please Provide]
Interactive Activities: For a more engaging experience, explore interactive online exercises that provide instant feedback and allow you to manipulate angles.
Video Tutorials: Visual learners may find video tutorials particularly helpful. Check out channels like:
Kuta Software (YouTube): Offers helpful videos like “Geometry- Parallel Lines And Transversals Part 2.” [Link to Kuta Software Video – Please Provide]
MaeMap (YouTube – vinteachesmath): Provides clear explanations and examples in videos such as “parallel lines and transversals (4 examples!).” [Link to MaeMap Video – Please Provide]
Real-World Applications
Parallel lines and transversals aren’t just theoretical concepts—they appear everywhere! Architects use them in building design, engineers rely on them for constructing bridges and roads, and artists use them to create perspective in their artwork. Recognizing these real-world applications makes learning geometry more relevant and engaging.
Advanced Concepts & Ongoing Research
Once you’re comfortable with the basics, you can explore more complex ideas, such as proving that lines are parallel based on angle relationships. This involves using deductive reasoning and applying geometric theorems.
Current research in fields like cognitive psychology and mathematics education continues to explore how students learn geometric concepts, suggesting that visual aids and real-world examples can significantly enhance understanding. There’s still much to be discovered, highlighting the ever-evolving nature of mathematics!
Need Roman Numerals?
Need to quickly utilize Roman numerals in your document? Learn how to effortlessly insert them with our guide on roman numerals copy and paste.
Hello, My love for writing is rivaled only by my passion for in-depth research. While many may skim the surface, I dive deep, seeking the hidden gems of information that give a story texture and depth. Every word I write is backed by hours of exploration, ensuring that my work is not just compelling, but also meticulously accurate. Join me on a journey where every piece is a deep dive into the realms of knowledge and storytelling.
