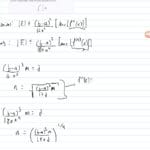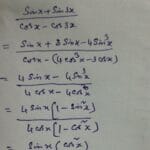Ready to conquer the integral of x sec(x)? This guide provides a clear, step-by-step approach using integration by parts, a powerful technique for tackling challenging integrals. We’ll also delve into strategically choosing ‘u’ and ‘dv’, the keys to successful integration. By the end, you’ll be equipped to handle x sec(x) and other similar integrals.
Integrating x sec(x) presents a unique challenge requiring the “integration by parts” technique. This method, derived from the product rule for derivatives but applied in reverse, helps transform tricky integrals into simpler forms. The formula is:
∫u dv = uv – ∫v du
Let’s apply this to x sec(x).
Choosing ‘u’ and ‘dv’
The first crucial step involves selecting ‘u’ and ‘dv’. A generally recommended strategy for integrals involving x and a trigonometric function is:
u = x
dv = sec(x) dx
This choice simplifies things because the derivative of ‘u’ (du) becomes dx. While integrating sec(x) might seem daunting, its integral is a known quantity: ln|sec(x) + tan(x)|.
Calculating ‘du’ and ‘v’
With ‘u’ and ‘dv’ defined, we calculate their counterparts:
du = dx (The derivative of u = x)
v = ln|sec(x) + tan(x)| (The integral of dv = sec(x) dx)
Applying the Formula
Substituting these values into the integration by parts formula:
This transforms the original integral into a simpler expression (x * ln|sec(x) + tan(x)|) and a remaining integral.
Handling the Remaining Integral
The integral ∫ln|sec(x) + tan(x)| dx is a “non-elementary integral.” It lacks a neat, closed-form solution using standard functions. However, numerical methods like Taylor series expansions or numerical integration can provide accurate approximations, especially within specific x ranges.
Thinking Beyond Formulas
Integrating xsec(x) isn’t always about finding a perfect answer. Sometimes, simplification and approximation are the goals. Current computational mathematics research continually seeks more efficient approximation methods for non-elementary integrals. The field is constantly evolving, and future techniques may offer more elegant solutions.
In summary, while a concise, closed-form solution for ∫ x sec(x) dx using elementary functions is unavailable, integration by parts simplifies the problem. Numerical methods then provide excellent approximations. This example demonstrates the importance of flexibility and varied approaches in mathematics.
Decoding the Integral of sec(x)
Integrating the secant function is a common challenge in calculus. The integral of sec(x) is often written as ln|sec(x) + tan(x)| + C. This formula helps measure the area under the secant curve. The “C” (constant of integration) reminds us that multiple functions can share the same derivative. Let’s consider some proofs:
Methods to Prove the Integral of secx
Proof #1: Trigonometric Manipulation
Multiply sec(x) by (sec(x) + tan(x))/(sec(x) + tan(x)).
Substitute ‘u’ for ‘sec(x) + tan(x)’.
The integral simplifies to ln|u| + C, which becomes ln|sec(x) + tan(x)| + C.
Proof #2: Tangent Substitution
Substitute ‘u’ for tan(x). ‘du’ becomes sec²(x) dx.
Rewrite sec(x) as √(1 + tan²(x)).
This yields ∫(1/√(1 + u²)) du, resulting in ln|tan(x + π/4)| + C. While seemingly different, it is equivalent to the original result.
Practical Applications of the Integral of sec(x)
The integral of sec(x) appears in various applications, including:
Calculating Arc Length: Determining the length of curved lines.
Finding Surface Area of Revolution: Calculating the surface area of shapes formed by rotating curves.
Calculating Volumes of Revolution: Determining volumes of solids formed by rotating curves.
Current research explores advanced integration techniques and their applications. Ongoing exploration suggests our understanding of integration will likely continue to evolve.
When dealing with the unique learning challenges presented by autism, consider exploring intraverbal aba. For those seeking to address involuntary seclusion in healthcare settings, a comprehensive understanding of its causes and effects can be gained through involuntary seclusion.
Derivatives of Trigonometric Functions: Mastering x sec(x)
Finding the derivative of xsec(x) requires the product rule because it involves two functions multiplied together.
Steps to find the Derivative of x secx
Step 1: Identify Functions
f(x) = x
g(x) = sec(x)
Step 2: Apply the Product Rule
h′(x) = f′(x) * g(x) + f(x) * g′(x)
Step 3: Calculate Individual Derivatives
f'(x) = 1
g'(x) = sec(x)tan(x)
Step 4: Substitute and Simplify
h′(x) = sec(x) + x sec(x)tan(x)
Thinking Beyond the Basics
This derivative is fundamental in calculus, and ongoing research explores its broader context and applications within areas like complex numbers, physics, and engineering. This calculation serves as a building block for advanced concepts in calculus.
Mastering the Integral of Sec(x): Substitution Techniques
Integrating sec(x) requires a substitution technique, transforming the integral into a solvable form.
The substitution method simplifies complex trigonometric integrals and reveals relationships between trigonometric functions, enabling integration of otherwise unsolvable functions. Current research may be exploring broader applications of this method.
This comprehensive guide has provided a deeper understanding of integrating and differentiating expressions involving sec(x). It emphasizes the importance of techniques like integration by parts and substitution, enabling you to solve complex calculus problems and appreciate the interconnectedness of mathematical principles. It also highlights the ever-evolving nature of mathematics, suggesting continued advancements and new perspectives in the future.
Hello, My love for writing is rivaled only by my passion for in-depth research. While many may skim the surface, I dive deep, seeking the hidden gems of information that give a story texture and depth. Every word I write is backed by hours of exploration, ensuring that my work is not just compelling, but also meticulously accurate. Join me on a journey where every piece is a deep dive into the realms of knowledge and storytelling.
