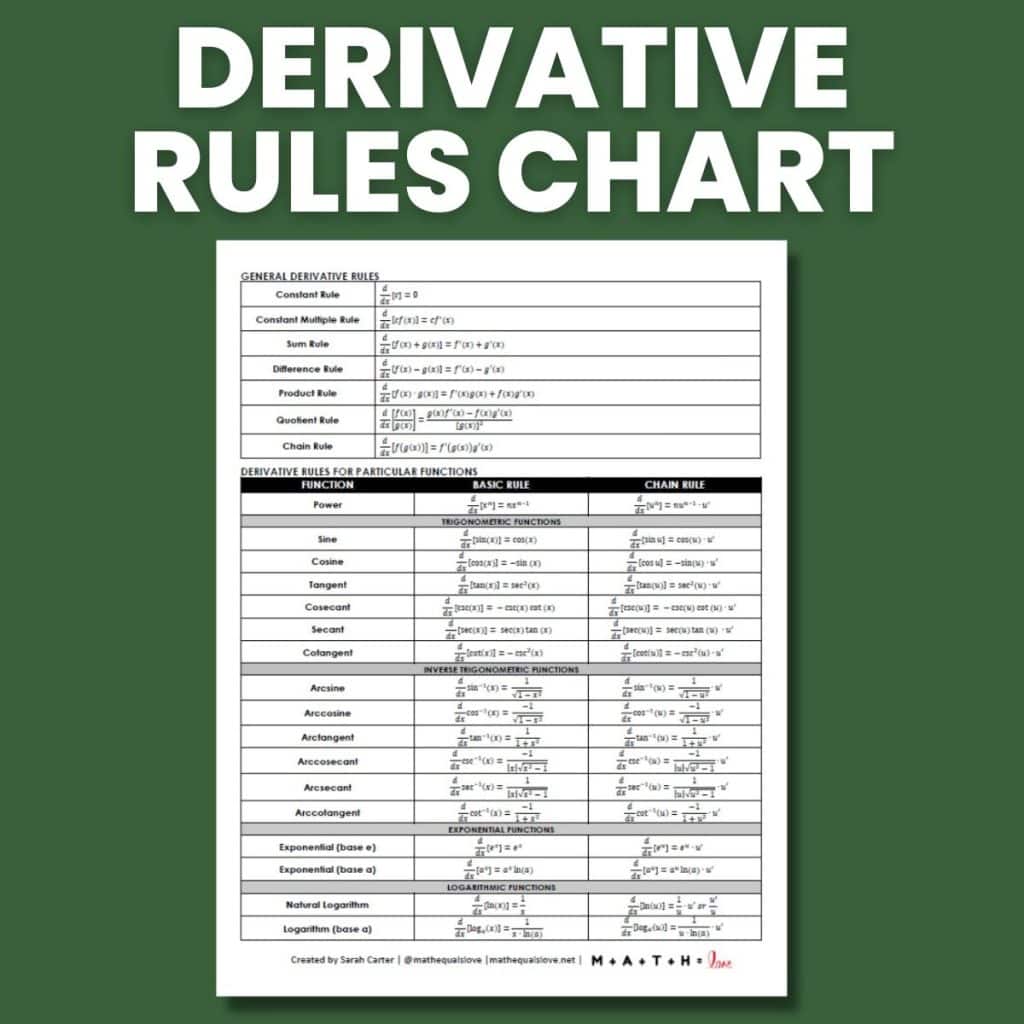
Conquer calculus with confidence! This cheat sheet provides a comprehensive collection of derivative rules and formulas, empowering you to tackle even the most challenging differentiation problems. From the power rule to the chain rule, we’ll unlock deeper understanding, moving beyond simple memorization to practical application in physics, engineering, and economics.
Essential Derivative Rules – Your Calculus Toolkit
Derivatives, at their core, describe the instantaneous rate of change of a function. Imagine the speedometer in your car—it tells you the derivative of your position with respect to time, or your instantaneous speed. Here’s your basic toolkit:
Foundational Rules
Power Rule: For functions like xⁿ, the derivative is nxⁿ⁻¹. For example, the derivative of x³ is 3x².
Constant Rule: The derivative of any constant (like 5, -2, or π) is always 0. A constant doesn’t change, so its rate of change is zero.
Constant Multiple Rule: For a function multiplied by a constant (cf(x)), the derivative is simply c times the function’s derivative (cf'(x)). The derivative of 3x² is 6x (3 multiplied by the derivative of x², which is 2x).
Sum/Difference Rule: When differentiating the sum or difference of functions, differentiate each function separately and then add or subtract the results. The derivative of x² + 2x is 2x + 2.
Product Rule: For functions multiplied together (f(x)g(x)), the derivative is f(x)g'(x) + g(x)f'(x). For x * sin(x), the derivative is sin(x) + xcos(x).
Quotient Rule: For functions divided by each other (f(x)/g(x)), the derivative is [g(x)f'(x) – f(x)g'(x)] / [g(x)]². Refer to a textbook for the full formula and examples as this can be a bit involved.
| Rule | Formula | Example |
|---|---|---|
| Power Rule | d/dx (xⁿ) = nxⁿ⁻¹ | d/dx (x³) = 3x² |
| Constant Rule | d/dx (c) = 0 | d/dx (5) = 0 |
| Constant Multiple Rule | d/dx (cf(x)) = cf'(x) | d/dx (3x²) = 6x |
| Sum/Difference Rule | d/dx (f(x) ± g(x)) = f'(x) ± g'(x) | d/dx (x² + 2x) = 2x + 2 |
| Product Rule | d/dx (f(x)g(x)) = f(x)g'(x) + g(x)f'(x) | d/dx (x * sin(x)) = sin(x) + xcos(x) |
| Quotient Rule | d/dx (f(x)/g(x)) = (g(x)f'(x) – f(x)g'(x)) / (g(x))² | See your textbook! |
Advanced Techniques
Chain Rule: Essential for composite functions (functions within functions), the chain rule states: differentiate the outer function, leaving the inner untouched, then multiply by the derivative of the inner function. This is crucial for functions like (x² + 1)³.
Implicit Differentiation: Used when y isn’t explicitly defined in terms of x (e.g., x² + y² = 1), this technique allows you to find dy/dx.
Higher-Order Derivatives: These are derivatives of derivatives. The second derivative (f”(x)) describes how the rate of change itself is changing (like acceleration).
Derivatives of Specific Functions – A Quick Reference
| Function | Derivative |
|---|---|
| xⁿ | nx^(n-1) |
| sin(x) | cos(x) |
| cos(x) | -sin(x) |
| tan(x) | sec²(x) |
| arcsin(x) | 1/√(1-x²) |
| arccos(x) | -1/√(1-x²) |
| arctan(x) | 1/(1+x²) |
| eˣ | eˣ |
| ln(x) | 1/x |
| sinh(x) | cosh(x) |
| cosh(x) | sinh(x) |
| tanh(x) | sech²(x) |
| arcsinh(x) | 1/√(x²+1) |
| arccosh(x) | 1/√(x²-1) |
| arctanh(x) | 1/(1-x²) |
Applications of Derivatives – Real-World Impact
Derivatives are powerful tools with wide-ranging applications:
- Optimization: Finding maximum or minimum values, crucial in fields like engineering and economics.
- Related Rates: Analyzing interconnected rates of change (e.g., a ladder sliding down a wall).
- Curve Sketching: Understanding function behavior through critical points and concavity.
- Physics: Velocity and acceleration are derivatives of position with respect to time.
- Engineering: Optimizing designs and analyzing stress/strain.
- Economics: Calculating marginal cost and marginal revenue.
Visualizing Derivatives – Graphical Insights
Derivatives can be visualized on graphs, providing a deeper understanding of their meaning and behavior. Tools like Desmos allow for dynamic exploration of functions and their derivatives.
- Positive Derivative: The original function is increasing (like climbing a hill).
- Negative Derivative: The original function is decreasing (sliding down a hill).
- Zero Derivative: Suggests a potential maximum, minimum, or point of inflection.
| Feature | Original Function Graph | Derivative Graph |
|---|---|---|
| Increasing function | Line sloping upwards | Horizontal line above x-axis |
| Decreasing function | Line sloping downwards | Horizontal line below x-axis |
| Local Maximum/Peak | Top of a curve | Crosses x-axis from positive to negative |
| Local Minimum/Valley | Bottom of a curve | Crosses x-axis from negative to positive |
| Constant Function | Horizontal line | Horizontal line at y=0 (the x-axis) |
| Point of Inflection | Where the curve changes concavity | Local maximum or minimum on the derivative graph |
This visual approach is incredibly helpful for understanding concepts like velocity and acceleration in physics or marginal analysis in economics. While we’ve made significant strides in visualizing derivatives, ongoing research suggests there may be more to uncover.
Why a Derivative Cheat Sheet Matters
This cheat sheet is designed to be a quick reference and learning tool. While not a replacement for deep understanding, it aids in:
- Quick Recall: Easily access essential formulas.
- Reinforced Learning: Regular review strengthens memory.
- Problem-Solving: Focus on application, not memorization.
- Exam Preparation: A valuable review tool.
Remember, active learning is key. Combine this cheat sheet with practice to truly master calculus. Consider exploring related concepts like isometric projection or trying a DNA triplet crossword to broaden your scientific knowledge.
- Unlock Water’s Symbolism: A Cross-Cultural Exploration - April 20, 2025
- Identify Black and White Snakes: Venomous or Harmless? - April 20, 2025
- Unlocking Potential: Origins High School’s NYC Story - April 20, 2025