This guide provides a comprehensive overview of Cyclic Coordinate Descent (CCD), an optimization algorithm used in various fields like machine learning, robotics, and statistical computing. We’ll explore its core concepts, variations, advantages, limitations, and ongoing research.
Decoding CCD: The Basics
Imagine navigating a complex, multi-dimensional landscape to find its lowest point. CCD simplifies this search by focusing on one direction at a time. It’s a methodical approach, akin to adjusting one knob at a time on a complex machine until it runs smoothly.
Key Points of Cyclic Coordinate Descent (CCD):
How CCD Works
- Initialization: Begin with an initial guess for the values of all variables.
- Coordinate Selection: Choose a single coordinate direction (variable) to adjust.
- Line Search: Find the best possible value for the selected variable along that direction, keeping all other variables constant. This often involves a “line search” to determine the optimal step size. Explore our coulomb’s law calculator for more insights into optimizing calculations.
- Iteration: Repeat steps 2 and 3 for every variable, cycling through them iteratively. This constitutes one cycle.
- Termination: Continue cycling until a pre-defined stopping condition is met. Common stopping criteria include a maximum number of cycles or a threshold for improvement.
Variations of CCD
CCD comes in several variations, primarily differing in how they select the coordinate to update:
- Cyclic CCD: Coordinates are updated in a fixed, predetermined order. This approach offers predictability and ease of implementation.
- Randomized CCD: Coordinates are selected randomly for each update. This can help escape local minima, those deceptive valleys that aren’t the lowest point overall. Some experts believe this randomized approach might offer advantages in certain scenarios.
Exploring Cyclic Coordinate Descent in Depth
Cyclic Coordinate Descent (CCD) offers a practical and often efficient approach to optimization problems, especially in high-dimensional spaces. Its iterative nature allows it to gradually refine a solution by focusing on one coordinate at a time.
Why Choose CCD?
- Simplicity: CCD is relatively straightforward to understand and implement, even for complex problems. Its step-by-step nature makes it easier to grasp than more intricate methods.
- Scalability: It scales well to high-dimensional problems, where other methods might struggle. This makes it valuable for tasks involving large datasets.
- Versatility: CCD can be applied to both smooth (differentiable) and jagged (non-differentiable) functions. This adaptability expands its range of applications.
Convergence and Performance
The performance of CCD depends on several factors: the specific problem, the “shape” of the function being minimized, and the coordinate selection strategy. In situations where variables are relatively independent, CCD might even outperform gradient descent, a more commonly used optimization technique. However, it’s important to note that current research suggests ongoing investigation is needed to fully understand these conditions.
Implementation Considerations
- Line Search: Techniques like the Golden Section Search or Brent’s Method are commonly employed for the line search step, optimizing the step size along each coordinate direction.
- Stopping Criteria: Carefully choosing stopping criteria is essential to balance computational cost and solution quality. While a maximum number of cycles provides a simple limit, more sophisticated methods consider the rate of improvement.
Looking Ahead: The Future of CCD
Research in CCD continues to explore:
- Advanced Coordinate Selection: Strategies beyond cyclic and randomized selection are being investigated, potentially leading to faster convergence.
- Line Search Refinements: Improving line search techniques could further enhance CCD’s efficiency.
- Hybrid Approaches: Combining CCD with other optimization methods might yield even more powerful algorithms.
Cyclic Coordinates: Unveiling Hidden Symmetries
Cyclic coordinates are special coordinates in a physical system that do not explicitly appear in the system’s energy equations (Lagrangian or Hamiltonian). Their absence suggests the presence of a conserved quantity, something that remains constant over time, such as momentum or angular momentum.
Understanding Cyclic Coordinates
- Definition: A coordinate that does not explicitly appear in the Lagrangian or Hamiltonian of a system.
- Implication: The existence of a cyclic coordinate suggests a conserved quantity associated with that coordinate.
- Identification: Cyclic coordinates are identified through the Euler-Lagrange or Hamiltonian equations.
- Examples: The azimuthal angle in a spherical pendulum or the angular position in a central force problem.
Importance of Cyclic Coordinates
- Simplified Equations: Fewer variables in the equations of motion make them simpler to solve and analyze.
- Revealing Symmetries: They highlight the underlying symmetries present in the system, offering valuable insights into its fundamental principles.
- Identifying Conserved Quantities: They directly point to conserved quantities, such as momentum or angular momentum, facilitating analysis and prediction of the system’s behavior.
Ongoing Research and Nuances
While the core principles of cyclic coordinates are well-established, ongoing research continues to explore their nuances and implications, especially in systems with approximate symmetries. There is some debate about the most effective approaches in such cases.
Coordinate Descent vs. Gradient Descent: Choosing the Right Tool
Both coordinate descent and gradient descent are optimization algorithms, but they differ in their approaches and strengths. Choosing the right one depends on the specific problem and data characteristics.
Coordinate Descent: Advantages and Disadvantages
Advantages:
- Excels with high-dimensional and sparse data.
- Easy to implement.
- Lower computational cost per iteration.
- Can handle constraints directly.
Disadvantages:
- Can be slow to converge, especially with highly correlated variables.
- May get stuck in local minima for non-convex functions.
Gradient Descent: Advantages and Disadvantages
Advantages:
- Fast convergence for smooth, unconstrained problems.
- Efficient for dense data.
Disadvantages:
- Struggles with sparse data.
- More complex to implement, especially with constraints.
- Higher computational cost per step.
Making the Right Choice
There is no universally “better” algorithm. Coordinate descent is likely a better choice for high-dimensional, sparse data with many variables and potential constraints. Gradient descent is probably more suitable for smaller, denser data and smoother, unconstrained problems. The optimal choice depends on the specific challenge you face. Ongoing research continues to refine both methods and explore hybrid approaches.
Key Points of Cyclic Coordinate Descent (CCD):
- Definition: An optimization algorithm that minimizes a function by sequentially optimizing along each coordinate direction.
- Steps: Initialize, select coordinate, perform line search, iterate, and terminate.
- Variations: Cyclic CCD and Randomized CCD.
- Advantages: Simplicity, scalability, versatility.
- Convergence and Performance: Problem-dependent, can outperform gradient descent under specific conditions.
- Implementation Details: Line search and stopping criteria.
- Ongoing Research: Advanced coordinate selection, line search methods, and hybrid approaches.
This comprehensive guide aims to equip you with a solid understanding of Cyclic Coordinate Descent and its applications. Remember that optimization is a constantly evolving field, so continuous learning and exploration are crucial.
- Unlock Water’s Symbolism: A Cross-Cultural Exploration - April 20, 2025
- Identify Black and White Snakes: Venomous or Harmless? - April 20, 2025
- Unlocking Potential: Origins High School’s NYC Story - April 20, 2025

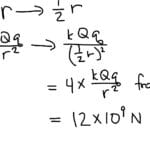














1 thought on “Cyclic Coordinate Descent: A Practical Guide to Optimization”
Comments are closed.