This guide provides a comprehensive understanding of conversion factors, their application in problem-solving, and specific guidance for your Lab 2 report. We’ll cover everything from basic definitions to real-world applications, ensuring you’re well-equipped to tackle any unit conversion challenge.
Decoding Conversion Factors
What are Conversion Factors?
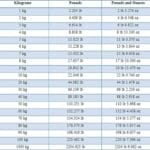
Imagine needing 2 cups of flour for a recipe, but your measuring cup only shows milliliters. A conversion factor is your solution. It’s a ratio expressing the equivalent values of two different units. For example, 1 cup equals approximately 237 milliliters. This relationship, written as 237 mL/1 cup or 1 cup/237 mL, is your conversion factor. It lets you switch between units without changing the actual amount.
Why are Conversion Factors Important in Lab 2?
In chemistry, precise measurements are crucial. Conversion factors become indispensable when dealing with different units, enabling accurate calculations and meaningful data analysis. They are particularly useful in stoichiometry (calculating reactant and product quantities) and density calculations (mass/volume relationships). In Lab 2, you’ll likely encounter various scenarios requiring unit conversions, making mastery of conversion factors essential for accurate results and insightful conclusions.
Mastering Dimensional Analysis
Unit Conversions with Dimensional Analysis
Dimensional analysis is a systematic approach to problem-solving using conversion factors. It’s like planning a route on a map, ensuring you reach your desired unit destination. You multiply your given value by a series of conversion factors, strategically arranging them so unwanted units cancel out, leaving you with the units you need.
For instance, let’s convert 2500 milliliters (mL) to liters (L):
2500 mL * (1 L / 1000 mL) = 2.5 L
The “mL” units cancel, leaving the answer in liters.
Using Dimensional Analysis in Lab 2
Lab 2 problems will probably involve multiple conversions. Dimensional analysis provides a structured framework for these complex scenarios, guiding you through the steps and minimizing errors. It’s particularly useful for converting between different systems (e.g., metric to imperial) or calculating derived units like density.
Navigating the Metric System
Understanding Metric Prefixes
The metric system simplifies measurements by using prefixes to denote multiples or fractions of base units (meter, gram, liter). These prefixes represent powers of ten, streamlining conversions.
| Prefix | Symbol | Multiplier |
|---|---|---|
| kilo- | k | 1000 (10³) |
| hecto- | h | 100 (10²) |
| deka- | da | 10 (10¹) |
| base unit | 1 | |
| deci- | d | 0.1 (10⁻¹) |
| centi- | c | 0.01 (10⁻²) |
| milli- | m | 0.001 (10⁻³) |
| micro- | µ | 0.000001 (10⁻⁶) |
Metric Conversions in Lab 2
Lab 2 often involves converting within the metric system. For example, converting milligrams to grams or liters to milliliters. Understanding these prefixes and their corresponding multipliers is key to accurate and efficient conversions.
Conquering Density Calculations
Density Formula and Units
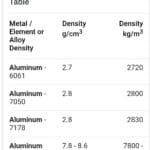
Density (ρ) measures how much mass (m) is packed into a given volume (V), expressed by the formula: ρ = m/V. Common units include g/mL, g/cm³, kg/m³.
Applying Conversion Factors in Density Problems
Calculating density may require converting mass and volume to consistent units. Conversion factors, along with dimensional analysis, help you align units before applying the density formula. Suppose you’re given a mass in kilograms and a volume in milliliters; you may need to convert the mass to grams and the volume to liters for consistency.
Check out our density aluminum lb in3 converter for quick density unit conversions.
Solving Lab 2 Report Sheet Questions: Step-by-Step
- Identify Units: Determine your starting and desired units.
- Find Conversion Factors: Identify the necessary conversion factors linking the units.
- Dimensional Analysis Setup: Arrange the problem using dimensional analysis, ensuring unwanted units cancel.
- Calculate and Round: Perform the calculation and round to the correct number of significant figures.
Example: Convert 15 inches to centimeters (1 inch = 2.54 cm)
15 in * (2.54 cm / 1 in) = 38.1 cm
Real-World Applications of Conversion Factors
Conversion factors extend beyond the lab. They’re used in:
- Cooking: Adjusting recipes, converting between measurement systems.
- Finance: Currency exchange, calculating interest rates.
- Engineering: Designing structures, ensuring precise measurements.
- Healthcare: Determining medication dosages, analyzing patient data.
- Everyday Life: Converting between metric and imperial units (e.g., miles to kilometers).
Beyond the Basics: Uncertainty and Ongoing Research
While we strive for accuracy, some conversion factors are approximations, introducing uncertainty. Ongoing metrology research refines our understanding of units and their relationships, potentially leading to future revisions. Also, some fields have specific conversion conventions. Researching and using appropriate context-specific conversions demonstrates a thorough understanding.
Conclusion
This guide provides a robust foundation in conversion factors and problem-solving for Lab 2 and beyond. Remember, practice solidifies understanding. Tackle those practice problems, explore further, and you’ll be converting units with confidence in no time. This knowledge also empowers you to critically evaluate data and calculations, a crucial skill in any scientific endeavor.