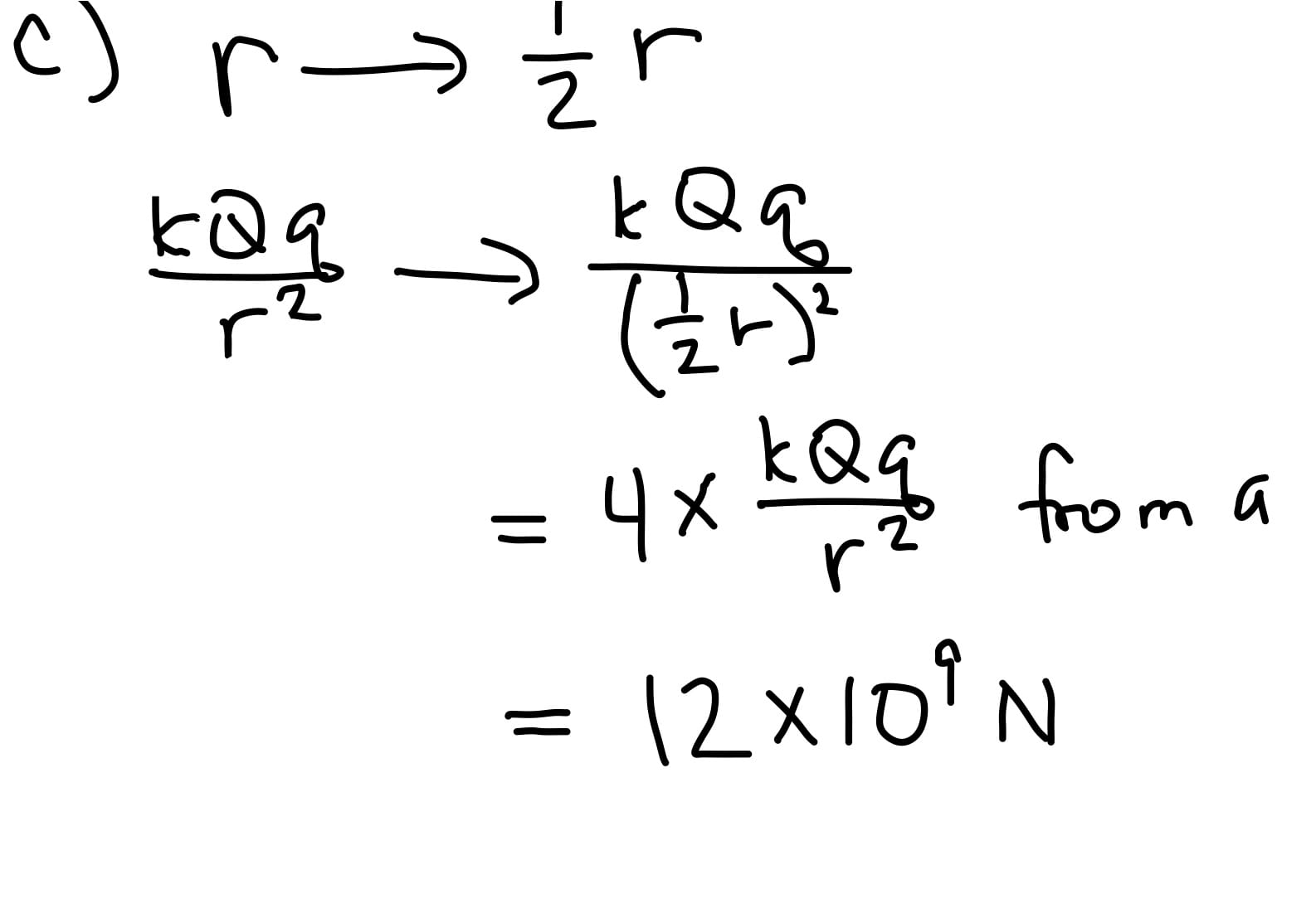Delve into the fascinating world of electrostatics with this comprehensive guide to Coulomb’s Law. We’ll explore the fundamental principles governing charged particle interactions and introduce you to the power of a Coulomb’s Law calculator. From simple demonstrations like static cling to complex applications in nanotechnology, understanding Coulomb’s Law unlocks insights into the forces shaping our world.
Decoding Coulomb’s Law: How Charges Interact
Ever wonder why a balloon sticks to the wall after you rub it on your hair? Or how dust clings to a computer screen? The answer lies in electrostatic forces, and Coulomb’s Law is the key to understanding them. This law, named after French physicist Charles-Augustin de Coulomb, quantifies the force between two charged particles. It tells us that this force is directly proportional to the product of the charges and inversely proportional to the square of the distance between them.
The Coulomb’s Law Formula: Unlocking the Math
Coulomb’s Law is elegantly expressed in the following equation:
F = k * |q1 * q2| / r²
Where:
- F: Represents the electrostatic force (measured in Newtons, N).
- k: Is Coulomb’s constant, approximately 8.98755 × 10⁹ N⋅m²/C². This constant is related to the permittivity of free space (ε₀), a fundamental constant describing the electric field’s interaction with a vacuum.
- q1 and q2: Represent the magnitudes of the two charges (measured in Coulombs, C). The vertical bars (| |) indicate that we use the absolute values of the charges, as we determine the direction separately.
- r: Is the distance between the centers of the two charges (measured in meters, m). Note that the force decreases rapidly with increasing distance, dropping to one-fourth if the distance is doubled.
Attraction and Repulsion: The Dance of Charges
Just like magnets, like charges (both positive or both negative) repel each other, while opposite charges attract. The direction of the force is along the line connecting the centers of the charges.
The Coulomb’s Law Calculator: Your Electrostatic Toolkit
Calculating electrostatic forces manually can be tedious, especially with multiple charges. This is where the Coulomb’s Law Calculator becomes invaluable. It simplifies complex calculations, handles unit conversions, and provides quick results—a powerful tool for students, educators, and professionals alike.
From Simple to Complex: Exploring Calculator Capabilities
Basic calculators allow you to input charge magnitudes (q1, q2) and distance (r) to determine the resulting force. More advanced versions can solve for any variable (F, q1, q2, or r) given the other three, offering impressive flexibility. Specialized calculators might even incorporate permittivity for different media, exploring how the surrounding material influences the force.
Coulomb’s Law in Action: Real-World Applications
Coulomb’s Law isn’t confined to textbooks. Its principles are at play in a surprisingly wide range of applications:
- Xerox Machines and Laser Printers: These devices use electrostatic forces to transfer toner particles from drum to paper, creating crisp images.
- Powder Coating: Electrostatic charging ensures a uniform and durable coating on various materials, from appliances to car parts.
- Air Purifiers: Many air purifiers use charged filters to attract and trap airborne particles, cleaning the air we breathe.
- Substance Solubility: Coulomb’s Law governs interactions between charged ions and water molecules, explaining why substances like salt readily dissolve.
- Static Cling: The simple act of a balloon sticking to a wall after being rubbed on your hair demonstrates charge separation and Coulombic attraction.
Advanced Techniques: Mastering the Calculator
For more complex scenarios involving multiple charges or non-linear arrangements, the following techniques can be extremely useful:
- Superposition Principle: When dealing with multiple charges, calculate the force between each pair individually, then add these forces vectorially to find the net force on a specific charge.
- Vector Components: Resolve forces into their x and y components to simplify calculations, especially when charges aren’t aligned along a single axis.
- Graphing Calculators: Some advanced calculators offer visual representations of forces and electric fields, providing greater insight into complex interactions. This can be especially helpful for understanding how forces change as charges move or how multiple charges contribute to the net force.
Using the Calculator Effectively: Tips and Tricks
- Unit Consistency: Always ensure consistent units (Coulombs, meters, Newtons) to avoid errors.
- Significant Figures: Report your final answer with the appropriate number of significant figures, reflecting the precision of your input data.
- Sanity Checks: Verify that the magnitude and direction of the calculated force make sense given the charges and their arrangement. Does a strong force between small, distant charges seem reasonable? Probably not.
Beyond the Basics: Exploring Further
While Coulomb’s Law provides a strong foundation for understanding electrostatics, it’s important to acknowledge its limitations. The law primarily applies to point charges (or charges with spherical symmetry) and static charges (charges at rest). In reality, charge distributions can be complex, and charges are often in motion.
Researchers continue to explore the nuances of electrostatic interactions, especially at very small scales or in specific materials. Some theorists suggest refinements to the classical Coulomb’s Law under these circumstances, and ongoing research seeks a more comprehensive understanding of electromagnetism.
Exploring the cyclic coordinate descent algorithm can also be valuable, as it provides an efficient optimization technique for minimizing complex functions, potentially relevant in advanced electrostatic calculations.
Remember, while the Coulomb’s Law calculator is a valuable tool, it’s essential to understand the underlying principles and limitations. By combining theoretical knowledge with practical application, you can unlock a deeper understanding of the fascinating world of electrostatics.
- Photocell Sensors: A Complete Guide for Selection and Implementation - April 2, 2025
- Discover Famous French Women: A History of Impact - April 2, 2025
- 2025 World Map: Unveiling Geopolitical Shifts & Risks - April 2, 2025